(7,4) Hamming Code - 编解码器实现与仿真
1. 编码原理 校验位的数量 假设原始数据块的长度为 $k$,校验位数为 $r$,那么要能够检测和定位所有 1-bit 错误的位置,必须满足以下不等式:
这个不等式的含义是:$2^r$ 种不同的校验结果必须能够表示:
$k$ 个数据位中可能出错的任一位
$r$ 个校验位中可能出错的任一位
以及无错误的情况(共 $k + r + 1$ 种)
对于 4-bit 的数据(即 $k = 4$),至少使用 3 位校验位
Hamming(7,4) 校验位通常放在整个码字中编号为 $2^0, 2^1, 2^2, \dots$ 的位置(即位置 1, 2, 4, 8,…)。
1 2 3 4 5 6 7 index: 7 6 5 4 3 2 1 bit : D4 D3 D2 P4 D1 P2 P1 各校验位的计算方式如下(奇校验): P1 = D1 ^ D2 ^ D4 P2 = D1 ^ D3 ^ D4 P4 = D2 ^ D3 ^ D4
码率是指每一位编码中实际承载有效信息的比例:
2. 编解码器的实现 hamming74_encoder 1 2 3 4 5 6 7 8 9 10 11 12 13 14 `timescale 1ns/1ps module hamming74_encoder ( input [3 :0 ] data_in, output [6 :0 ] code_out ); wire p1, p2, p3; assign p1 = data_in[0 ] ^ data_in[1 ] ^ data_in[3 ]; assign p2 = data_in[0 ] ^ data_in[2 ] ^ data_in[3 ]; assign p3 = data_in[1 ] ^ data_in[2 ] ^ data_in[3 ]; assign code_out = {data_in[3 :1 ], p3, data_in[0 ], p2, p1}; endmodule
hamming74_decoder 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 module hamming74_decoder ( input [6 :0 ] code_in, output [3 :0 ] data_out, output error, output [6 :0 ] corrected_code ); wire [2 :0 ] syndrome; reg [6 :0 ] corrected_data; assign syndrome[0 ] = code_in[0 ] ^ code_in[2 ] ^ code_in[4 ] ^ code_in[6 ]; assign syndrome[1 ] = code_in[1 ] ^ code_in[2 ] ^ code_in[5 ] ^ code_in[6 ]; assign syndrome[2 ] = code_in[3 ] ^ code_in[4 ] ^ code_in[5 ] ^ code_in[6 ]; assign error = |syndrome; always @(*) begin corrected_data = code_in; if (error) begin case (syndrome) 3'b001 : corrected_data[0 ] = ~code_in[0 ]; 3'b010 : corrected_data[1 ] = ~code_in[1 ]; 3'b011 : corrected_data[2 ] = ~code_in[2 ]; 3'b100 : corrected_data[3 ] = ~code_in[3 ]; 3'b101 : corrected_data[4 ] = ~code_in[4 ]; 3'b110 : corrected_data[5 ] = ~code_in[5 ]; 3'b111 : corrected_data[6 ] = ~code_in[6 ]; default : corrected_data = code_in; endcase end end assign corrected_code = corrected_data; assign data_out = {corrected_data[6 ], corrected_data[5 ], corrected_data[4 ], corrected_data[2 ]}; endmodule
3. 基于Verilator的仿真 开源高性能仿真器 Verilator 是一款功能强大的开源 Verilog/SystemVerilog 仿真工具 ,主要用于将 Verilog HDL 代码转换为高效的 C++ 或 SystemC 代码,以便进行快速仿真。
特性
Verilator VCS / ModelSim
类型
周期级仿真
事件驱动仿真
许可
开源(免费)
商业收费
运行速度
非常快
较慢,但精确
调试方式
基本 trace/VCD
强大的 GUI 波形调试
仿真原理
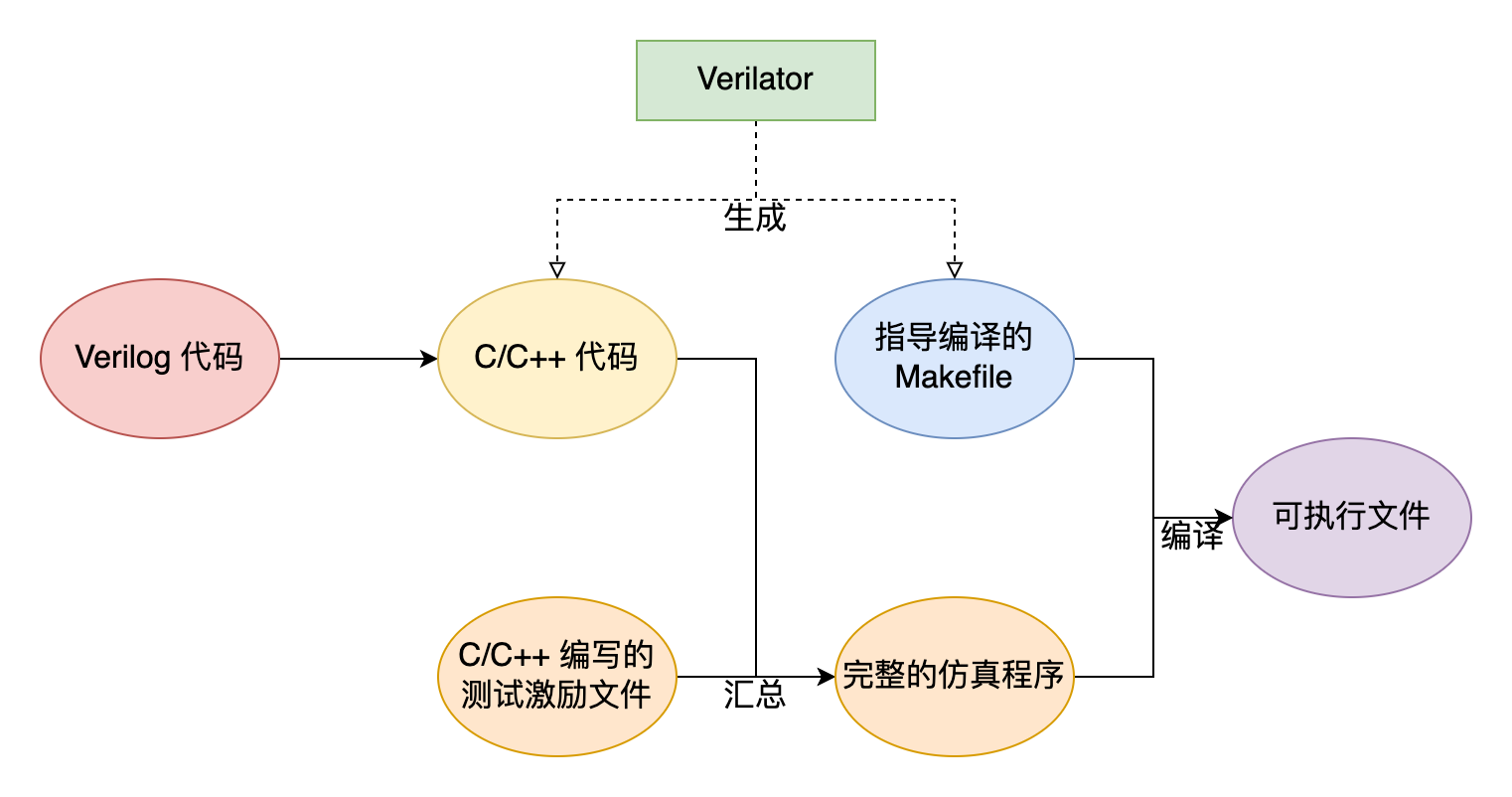
首先,Verilator 将 Verilog 代码中并行的各个逻辑部件以合适的顺序串行化,使硬件设计转化为一个类似于处理器模拟器的软件;
接着,使用 C/C++ 编写激励文件。Verilator 提供了顶层模块输入/输出引脚的接口,使我们得以对顶层模块的输入信号赋值或读取其输出信号。与 Vivado 仿真不同的是,我们可以实时地输出一些调试信息;要查看波形图时,需要导出波形文件;
最后,Verilator 会生成一个 Makefile 脚本,将生成的 C/C++ 文件和我们编写的激励文件编译成成用于仿真的可执行文件。
测试框架 提供独立的运行环境,实现 C/C++ 和 Verilog 的完全解耦,提高代码复用性和可移植性,可以兼容其他仿真软件(如 VCS)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 #define VTOP concat(V, TOP_NAME) class TESTBENCH {private : std::unique_ptr<VerilatedFstC> tfp; std::unique_ptr<VTOP> top; std::unique_ptr<VerilatedContext> contextp; public : TESTBENCH (void ); virtual ~TESTBENCH (void ); virtual void reset (void ) virtual void tick (void ) virtual void eval_and_dump (void ) virtual void sim (void ) virtual bool done (void ) };
新版 Verilator 的一些特性:调用仿真环境contextp,无需手动维护sim_time。
1 2 3 4 5 6 7 8 9 10 void TESTBENCH::eval_and_dump (void ) contextp->timeInc (1 ); top->eval (); tfp->dump (contextp->time ()); } void TESTBENCH::sim (void ) while (!done ()) eval_and_dump (); } bool TESTBENCH::done (void ) return (Verilated::gotFinish ()); }
编写基于 Verilog 的 testbench:
Verilator 的--timing选项对可以支持延时
相对于 C/C++ testbench,这样可以兼容其他仿真软件
对于 4 bits 的数据,需要验证 $2^7$ * 7 种单比特错误可以被成功纠正。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 for (i = 0 ; i < 16 ; i = i + 1 ) begin data_in = i[3 :0 ]; #1 ; for (err = 0 ; err <= 7 ; err = err + 1 ) begin error_position = err[2 :0 ]; noisy_code = code_out; if (error_position != 0 ) noisy_code[error_position - 1 ] = ~code_out[error_position - 1 ]; #1 ; $write ("%4b %7b %1d %7b %4b %1b" , data_in, code_out, error_position, noisy_code, data_decoded, error_flag); check(data_in, data_decoded); end end
加入 FST 波形跟踪:FST 格式比 VCD 更小更快 ,加载更快、占用更低 。需要 gtkwave 的支持。
1 2 3 4 5 6 7 8 9 #include <verilated_fst_c.h> TESTBENCH::TESTBENCH (void ) { contextp = std::make_unique <VerilatedContext>(); top = std::make_unique <VTOP>(contextp.get ()); Verilated::traceEverOn (true ); tfp = std::make_unique <VerilatedFstC>(); top->trace (tfp.get (), 99 ); tfp->open (TRACE_FILE (TOP_NAME, WAVE_TYPE)); }
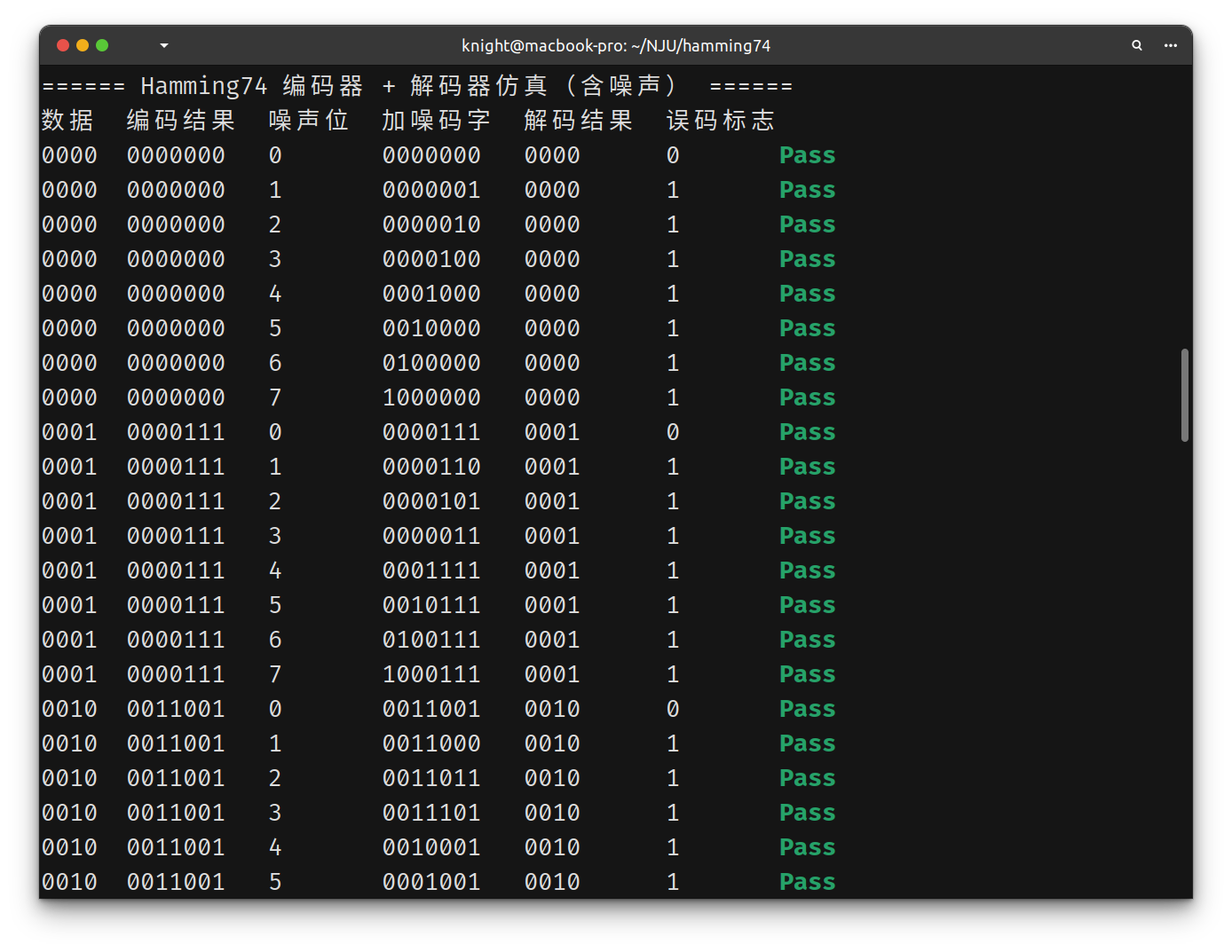
仿真结果 单 bit 错误均成功校正:
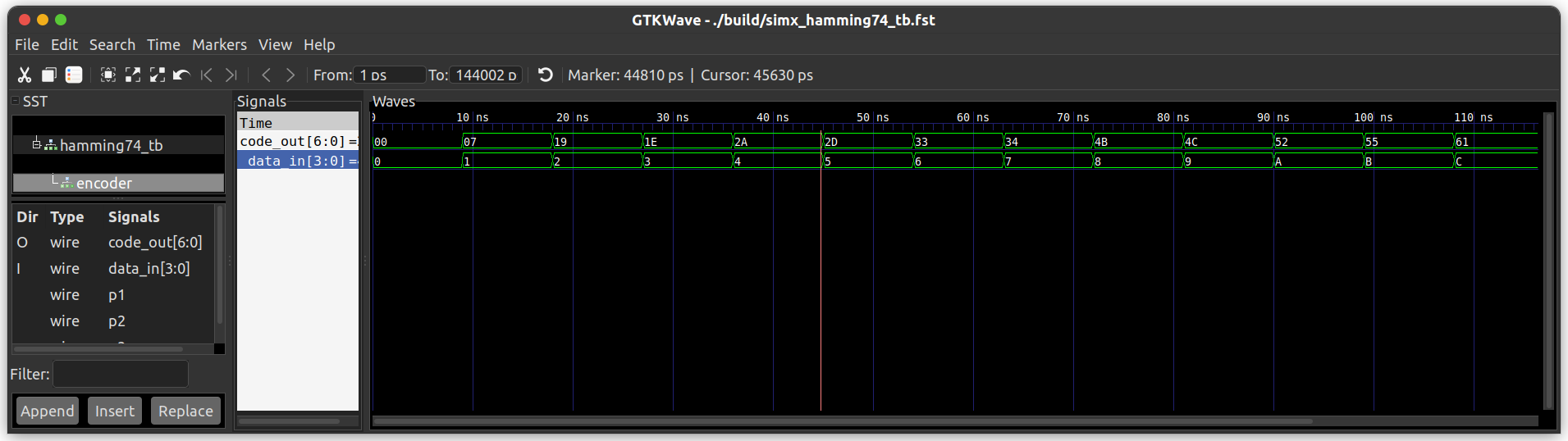
仿真波形 编码器:
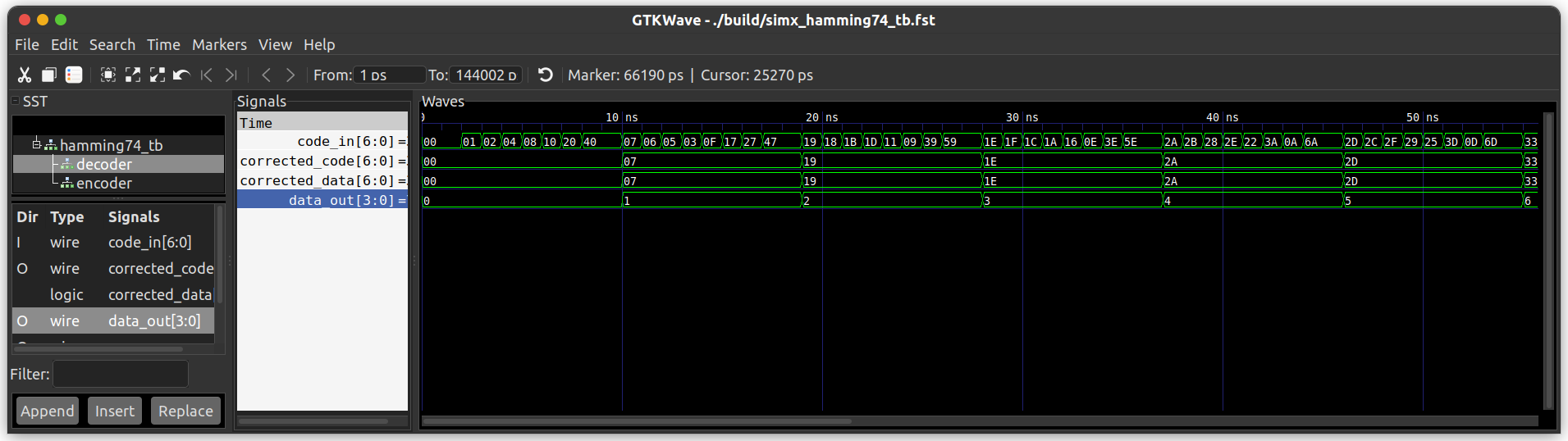
解码器:
4. 一个有趣的应用 bmp 图像的传输
一个基于 Hamming(7,4) 编码的图像传输仿真程序,模拟图像在传输过程中发生比特错误并尝试纠正的过程:
bmp 头部保护 :拷贝 BMP 图像文件头部 54 字节,确保输出图像仍保持合法。数据编码 :每个图像字节拆分为两个 4 位数据,分别使用 Hamming(7,4) 编码为 7 位码字。噪声模拟 :按设定概率对编码位随机翻转,模拟传输中的比特错误。纠错解码 :将含噪码字送入解码器,自动检测并纠正单比特错误,恢复原始数据。图像输出 :解码结果重组成图像并保存,同时输出一份仅加噪未纠错的图像,便于对比效果。
模拟信道噪声:
1 2 NOISE_RATE ?= 5 bmp: DEFINES += -DNOISE_RATE="$(NOISE_RATE) "
1 2 3 4 5 6 7 8 9 uint8_t invert_mask (int width) assert (width <= 8 && width > 0 ); uint8_t mask = 0 ; for (int i = 0 ; i < width; i++) { if (rand () % 100 < NOISE_RATE) mask |= (1 << i); } return mask; }
传输结果对比
左为未经纠错的图像,右为经过 74 Hamming 编解码器纠错的图像。
$\text{NOISE RATE} = 1 \%$
$\text{NOISE RATE} = 5\%$
$\text{NOISE RATE} = 10 \%$
$\text{NOISE RATE} = 20 \%$
总结
在信道噪声较低时,74 汉明码有不错的纠错效果,当噪声变大,一个字节串中出现大量的 2 bits 即以上的错误时,纠错效果明显变差。